Задача
Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежит куча камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в кучу один камень или увеличить количество камней в куче в два раза. Для того чтобы делать ходы, у каждого игрока есть неограниченное количество камней.
Игра завершается в тот момент, когда количество камней в куче становится не менее 29. Победителем считается игрок, сделавший последний ход, т.е. первым получивший кучу, в которой будет 29 или больше камней. style="text-align: justify;">В начальный момент в куче было S камней, 1 ≤ S ≤ 28.
Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника.
Укажите такое значение S, при котором Петя не может выиграть за один ход, но при любом ходе Пети Ваня может выиграть своим первым ходом.
Решение (аналитика)
Ходы, которые делают игроки, можно разделить на две группы: "сильные" (добавить в кучу один камень) и "слабые" (увеличить количество камней в куче в два раза). "Сильный" ход позволяет победить за меньшее количество ходов, "слабый" соответственно нет. Таким образом, чтобы Ване победить своим первым ходом ему необходимо делать "сильный" ход (увеличить количество камней в куче в два раза). Петя в свою очередь может сделать как "сильный" так и "слабый ход".
Составим дерево игры для описанной ситуации:
Таким образом получаем два возможных исхода игры:
Вариант 1.
Вариант 2.
Необходимо обратить внимание на то, что в задание есть уточнение: Ваня может выиграть своим первым ходом при любом ходе Пети. Очевидно, что Ваня не сможет выиграть своим первым ходом, если Петя сделает слабый ход из кучи с 8 камнями.
Куча с 14 камнями удовлетворяет всем условиям.
Ответ: 14.
Решение (электронная таблица)
Рассмотрим вариант решения задачи при помощи электронных таблиц (на примере MS Excel).
Создадим новый файл и обозначим столбцы, в которых будет указано начально положение (куча S), первый ход Пети, первый ход Вани.
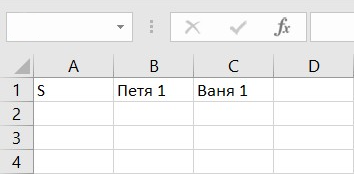
Петя может сделать два хода: +1 или *2. Запишем соответствующие формулы в ячейки В2 и В3.
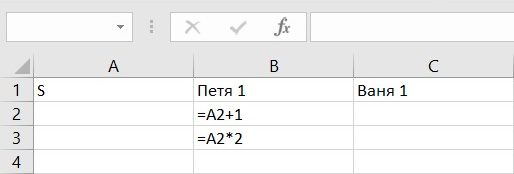
Ваня, для гарантированного выигрыша, будет увеличивать количество камней в куче в два раза. Запишем соответствующие формулы в ячейки С2 и С3.
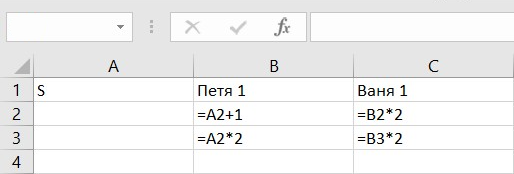
Для удобства нахождения решения, сделаем условное форматирование ячеек, отображающих первый ход Вани (С2 и С3).
Далее в ячейке А1 поочередно перебираем значения.
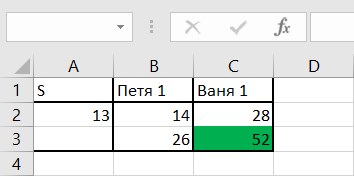
Значения перебираем до тех пор, пока ход Вани (С2 и С3) не окрасится в зеленый цвет.
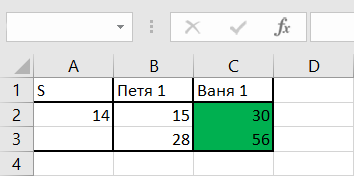
Ответ: 14.


















