Задача
Для игры, описанной в задании 19, найдите значение S, при котором одновременно выполняются два условия:
- у Вани есть выигрышная стратегия, позволяющая ему выиграть первым или вторым ходом при любой игре Пети;
- у Вани нет стратегии, которая позволит ему гарантированно выиграть первым ходом.
Если найдено несколько значений S, в ответе запишите минимальное из них.
Решение (аналитика)
У Вани есть выигрышная стратегия, которая позволяет ему выиграть либо первым, либо вторым ходом при любой игре Пети. Построим дерево игры для указанных случаев.
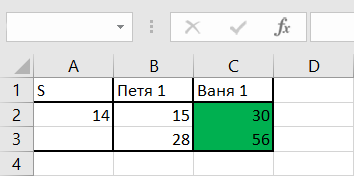
В задании 20 мы уже нашли решения для позиций, выделенных цветом:
В задании 20 мы получили пару: 7, 13.
13 камней можно получить только одним вариантом из 12 (+1), также как и 7 камней из 6 (+1).
В случае, если в куче было 6 камней, то Ваня не сможет выиграть ни первым, ни вторым ходом (стоит напомнить, что Ваня должен выиграть при любом ходе Пети).
В случае, если в куче было 12 камней, то Ваня сможет выиграть либо первым, либо вторым ходом.
Ответ: 12.
Решение (электронная таблица)
Продолжим решение задачи при помощи электронных таблиц (на примере MS Excel).
При решении задания 19 мы создали электронную таблицу, которая содержит динамические ссылки и при помощи перебора нашли необходимое количество камней.
На основании этой таблицы мы построили новую, которая помогла решить задание 20.
На основании данной таблицы построим новую.
В ячейку A13 внесем значение "S", это будет начальная позиция.
Затем скопируем предыдущую таблицу (диапазон A6:D10) в диапазон B13:E17.
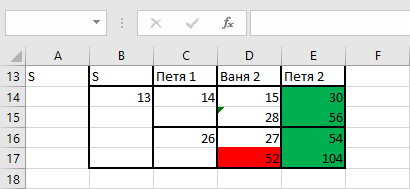
Скопируем диапазон B14:E17 в диапазон B18:E21.
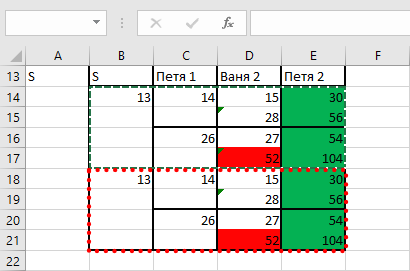
В ячейку В14 внесем формулу =A14+1, а в ячейку В18: =A14*2.
При помощи условного форматирование сделаем выделение ячеек C14, C16, C18, C20: если количество камней в них становится не менее 29, то они выделяются зеленым цветом (как это сделать смотрите в решении задачи 19).
Учитывая результат, полученный в задаче 20 (7, 13), необходимо проверить два значения: 6 и 12 (меньше на 1).
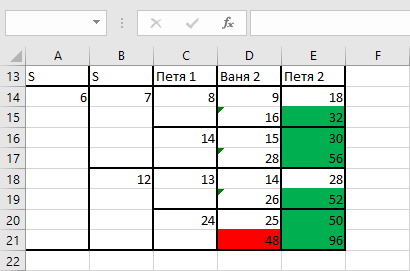
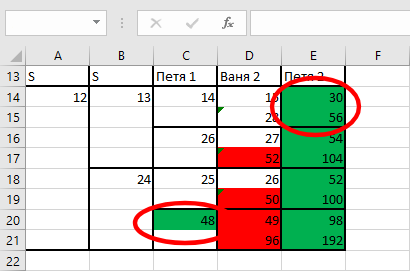
Ответ: 12.


















