Задача
Для игры, описанной в задании 19, найдите два таких значения S, при которых у Пети есть выигрышная стратегия, причём одновременно выполняются два условия:
- Петя не может выиграть за один ход;
- Петя может выиграть своим вторым ходом независимо от того, как будет ходить Ваня.
Найденные значения запишите в ответе в порядке возрастания.
Решение (аналитика)
Поскольку Петя не может выиграть после своего первого хода (после хода в куче получилось камней меньше чем 29), то получаем два возможных исхода этого события.
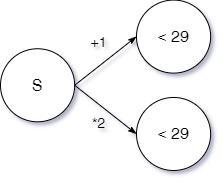
| Исход 1 | Исход 2 |
|
\[S+1 < 29\]
\[S < 28\]
|
\[2*S < 29\]
\[S <14,5 \]
|
Таким образом, изначально в куче было однозначно не более 14 камней.
Теперь рассмотрим первый ход Вани. Т.к. Ваня также не может выиграть своим первым ходом, но следующий игрок (Петя) выигрывает, то эту ситуацию можно рассмотреть по аналогии с предыдущей. Получаем также два исхода.
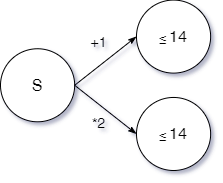
| Исход 1 | Исход 2 |
|
\[S+1 \leq 14\]
\[S \leq 13\]
\[S = 13\]
|
\[2*S \leq 14\]
\[S \leq 7\]
\[S = 7\]
|
Ответ: 7, 13.
Решение (электронная таблица)
Продолжим решение задачи при помощи электронных таблиц (на примере MS Excel).
При решении задания 19 мы создали электронную таблицу, которая содержит динамические ссылки и при помощи перебора нашли необходимое количество камней.
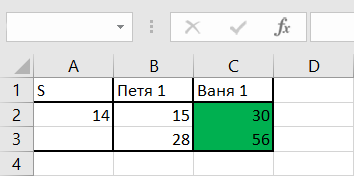
На основании этой таблицы построим новую.
В ячейку A6 внесем значение "S", это будет начальная позиция.
Затем скопируем предыдущую таблицу (диапазон A1:C3) в диапазон B6:D8.
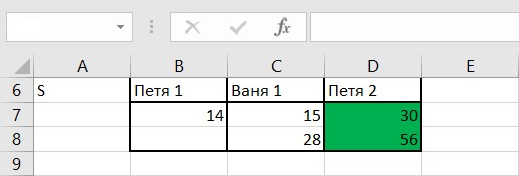
Скопируем диапазон B7:D8 в диапазон B9:D10.
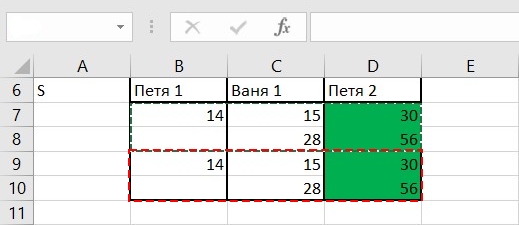
В ячейку В7 внесем формулу =A7+1, а в ячейку В9: =A7*2.
При помощи условного форматирование сделаем выделение ячеек: если количество камней в них становится не менее 29, то они выделяются красным цветом (как это сделать смотрите в решении задачи 19). Далее, при помощи перебора, находим интересующие нас значения.
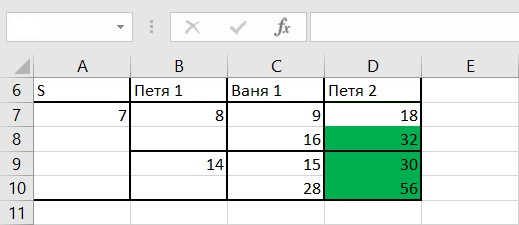
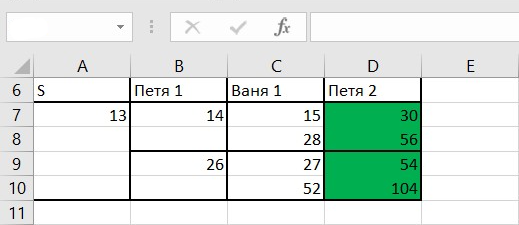Ответ: 7, 13.
