Задание
Между населёнными пунктами A, B, C, D, E построены дороги, протяжённость которых (в километрах) приведена в таблице.
Определите длину кратчайшего пути между пунктами A и Е, проходящего через пункт С. Передвигаться можно только по дорогам, протяжённость которых указана в таблице. Каждый пункт можно посетить только один раз.
Решение (граф)
Для решения этого задания, на основании представленной таблицы, построим граф, который называется деревом.
Изпункта А мы можем попасть в пункты B, C, D, E. На ветках дерева укажем протяженность дорог. Обратите внимание на то, что фактическая протяженность дорог не соответствует их графическому изображению!
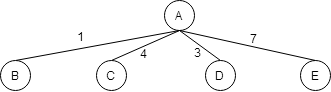
Рассмотрим пунк В.
Из пункта В можно попасть в пункты C и D.
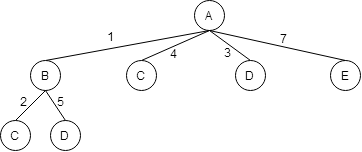
Из пункта С можно попасть в пункт D.
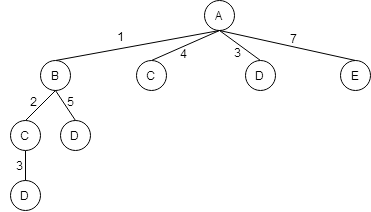
Из пункта D - в пункт E.
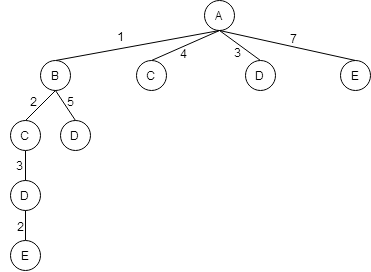
Теперь вернемся к пункту D, и которого можно попасть в пункт E.
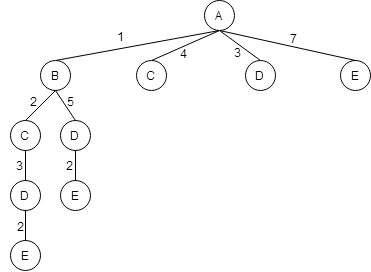
Рассмотрим пункт C.
Из пункта C можно попасть в пункт B и D.
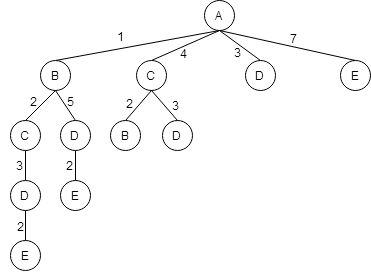
Из пункта можно попасть в пункт D.
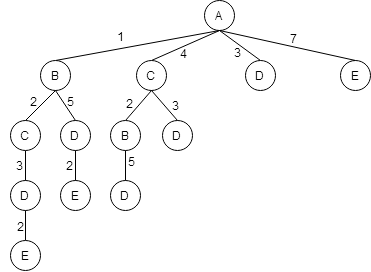
Из пункта D - в пункт E.
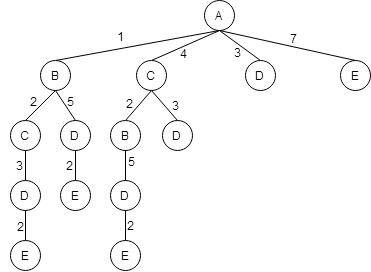
Возвращаемся к пункту D, из него попадаем в пункт E.
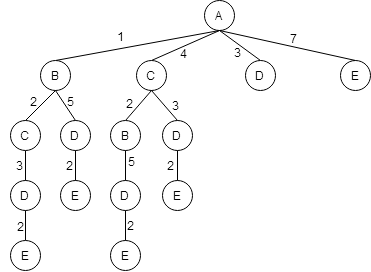
Рассмотрим пункт D.
Из пункта D можно попасть в пункты B, C и E.
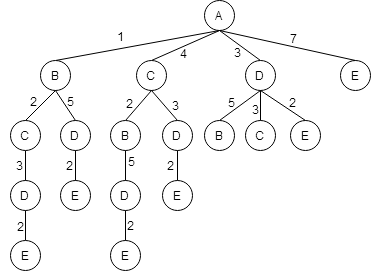
Из пункта B - в пункт С.
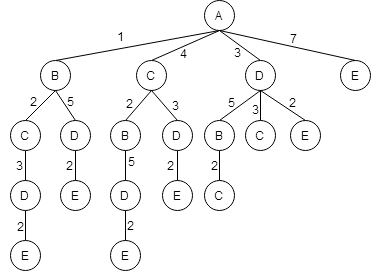Из пункта C - в пункт D.
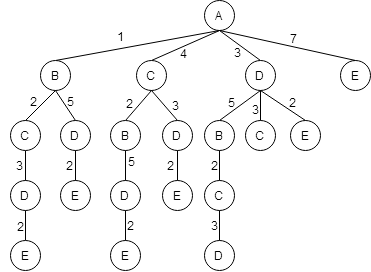
Из пункта D - в пункт E.
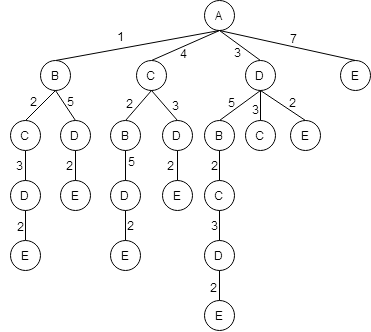
Вернемся к пункту C.
Из пункты С можно попасть в пункт D.
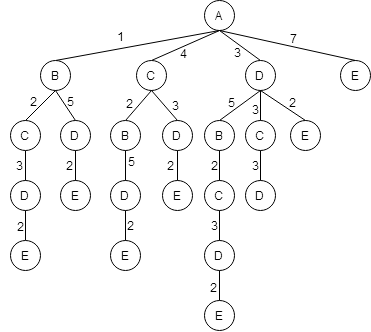
Из пункта D - в пункт E.
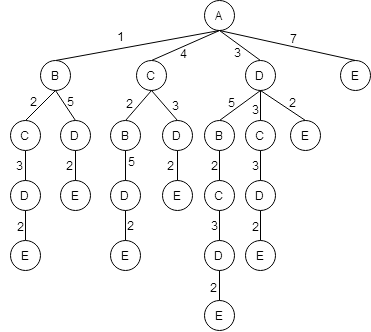
Мы построили дерево всех возможных путей из пункта A в пунк E, которое соответствует весовой таблице, представленной в условии задачи.
На следующем этапе необходимо подсчитать протяженность получившихся дорог.
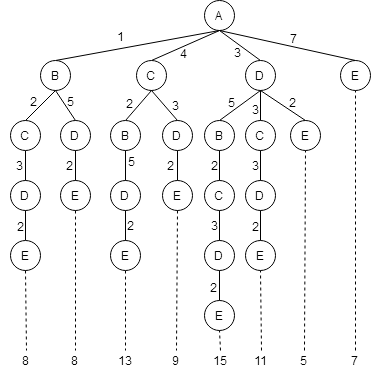
Согласно условию, дорога должна проходить через пункт C. Выделис те дороги, которые проходят через пункт C.
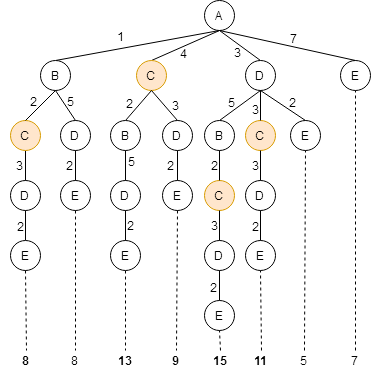
Из получившихся дорог выбираем ту, которая имеет наименьшую протяженность.
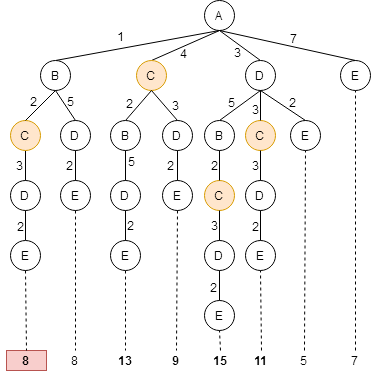
Ответ: 8.
Решение (Алгоритм Дейкстры)
Выпишем в отдельный список все возможные вершины графа.
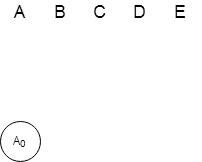
Будем строить дерево. Отметим стартовую вершину (в нашем случае это точка А) и подпишем рядом с ней расстояние, которое необходимо преодалеть, чтобы добраться до нее из стартовой точки А. То есть, 0. Это будет корень нашего дерева.
Из всех возможных вершин дерева найдем вершину с наименьшим числом (это вершина А) и вычеркнем эту вершину из списка доступных вершин. В дальнейшем мы ее расматривать не будем.
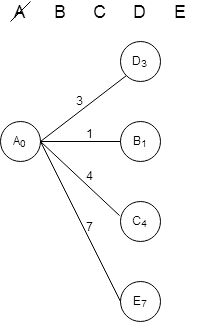
По таблице расстояний найдем все вершины, до которых идет дорога из текущей вершины и которые еще не вычеркнуты. Нарисуем ветви для каждой из найденных смежных вершин. На концах ветвей укажем названия вершин. На вервях подпишем длины ребер. Для каждой полученной вершины посчитаем расстояние (расстояние до текущей вершины плюс расстояние до каждой полученной вершины). Эти знаения запишем рядом с каждой вершиной.
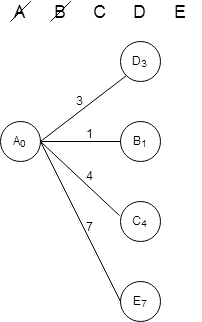
Среди конечных вершин найдем вершину с наименьшим расстоянием. Вычеркнем эту вершину из списка доступных вершин. Дальнейшее действие будем делать из нее.
По таблице расстояний найдем все вершины, до которых идет ребро из текущей вершины. Нарисуем из текущей вершины ветви дерева для каждой из найденных смежных вершин, нарисуем на концах ветвей названия этих вершин. Подпишем на ветвях длины ребер по таблице расстояний. Для каждой полученной вершины посчитаем расстояние до не.
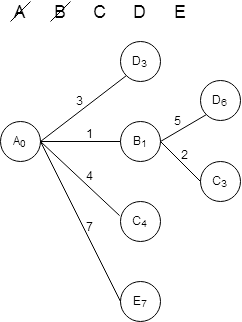
Среди конечных вершин найдем вершину с наименьшим расстоянием. Это вершины D и C. Так как по условию необходимо, что путь проходил через пункт С., то мы выбираем именно эту вершину. Вычеркиваем ее из списка доступных вершин. Дальнейшее действие будем делать из нее.
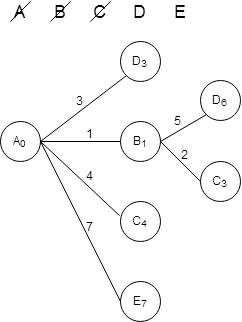
По таблице расстояний найдем все вершины, до которых идет ребро из текущей вершины. Нарисуем из текущей вершины ветви дерева для каждой из найденных смежных вершин, нарисуем на концах ветвей названия этих вершин. Подпишем на ветвях длины ребер по таблице расстояний. Для каждой полученной вершины посчитаем расстояние до не.
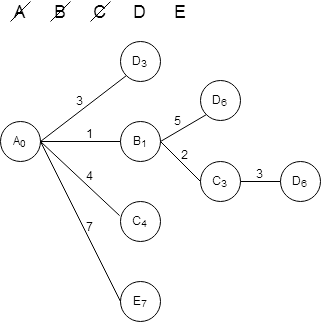
В нашем случае эта вершина D. Мы будем продолжать строить дерево из этой вершины. Вычеркиваем ее из списка доступных вершин. Дальнейшее действие будем делать из нее.
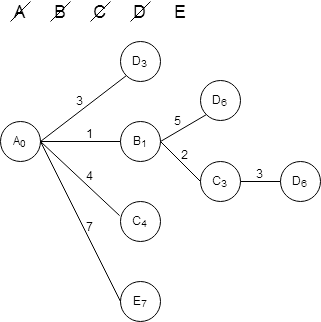
По таблице расстояний найдем все вершины, до которых идет ребро из текущей вершины. Нарисуем из текущей вершины ветви дерева для каждой из найденных смежных вершин, нарисуем на концах ветвей названия этих вершин. Подпишем на ветвях длины ребер по таблице расстояний. Для каждой полученной вершины посчитаем расстояние до не.
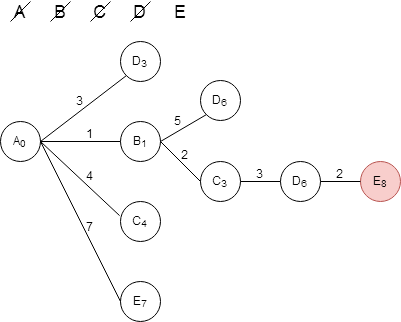
Ответ: 8.
