Задание

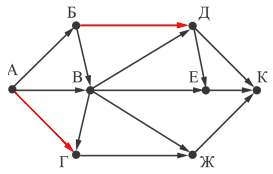
На рисунке – схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж и К. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город К, проходящих через город В?

Решение

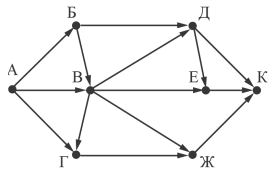
Обратите внимание на то, что схема дорог, связывающих города. представлена в виде ориентированного графа.

Начнем с теории.

Если в город Е из города A можно добраться только из городов B, C и D, то количество различных путей из города A в город E (N_E) равно сумме числа различных путей из A в B (N_B), из A в C (N_C) и из A в D (N_D).

В начальной вершине количество дорог равно 1 (1 путь из А в А, никуда не надо ехать).

Вернемся к нашей задаче.

Для решения задачи мы будем указывать количество дорог для пункта на рисунке.

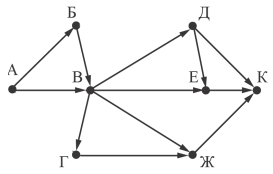
Нас интересуют пути, проходящие через город В, поэтому на первом этапе необходимо убрать все ребра (можно просто их перечеркнуть), которые позволяют на пути от А к К обойти город В: это рёбра БД, АГ.

В начальной вершине количество дорог равно 1.

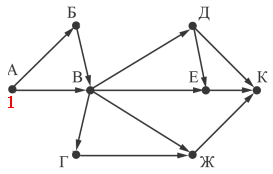
В вершину Б можно приехать только из А, поэтому помечаем ее тоже - 1. В вершину В можно приехать из А и Б - 2 (1+1).

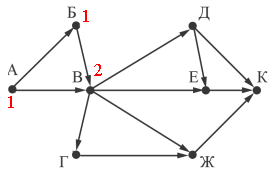
В вершину Д и Г можно приехать только из В, поэтому помечаем их тоже - 2.

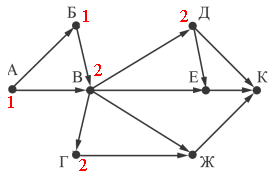
В вершину Е можно приехать из Д и В - 4 (2+2), а в вершину Ж можно приехать из Г и В - 4 (2+2).

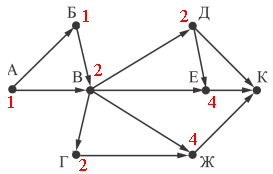
Таким образом, в вершину К можно приехать из Д, Е и Ж - 10 (4+4+2).

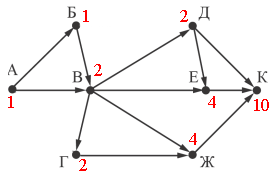
Ответ: 10.

Стоит обратить внимание на то, что данную задачу можно решить записывая рассуждения следующим образом:

А=1
В=Б=1
В=Ф+Б=1+1=2
Г=В=2
Д=В=2
Е=В+Д=2+2=4
Ж=Г+В=2+2=4
К=Д+Е+Ж=4+4+2=10