Задача 2
Тогда первому столбцу соответствовала бы переменная y, а второму столбцу – переменная x. В ответе следовало бы написать: yx
Внешним действием (последним выполняемым) в исходном выражении является дизъюнкция:
¬x ∨ y ∨ (¬z ∧ w)
Вспомним, что из себя представляет дизъюнкции (логическое сложение): сложное логическое выражение, которое истинно тогда, когда истинно хотябы одно из входящих простых высказывания (операнд).
Какой из операндоб будет равняться еденице (истина) или нулю (ложь) сложно: ¬x = 1 или 0, y = 1 или 0, ¬z ∧ w = 1 или 0.
Функция же ложна только в одном случае, — когда все операнды ложны. Поэтому будем искать по признаку лжи.
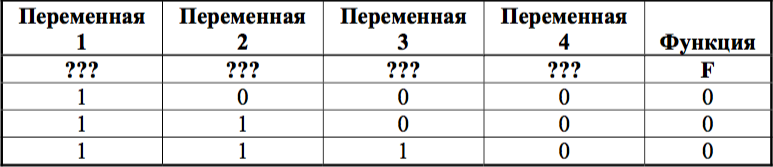
В исходной таблице истинности во всех строках функция ложна. Чтобы понять в каком столбце должна находиться та или иная переменная, возьмем за основу строку, в которой только одна единица или только один нуль.
Строка №1: в ней одна единица — первый столбец. В исходном выражении, чтобы функция была ложна, необходимо, чтобы ¬x = 0, иными словами x = 1. Значит первый столбец соответствует переменной x.
| Перем. 1 | Перем. 2 | Перем. 3 | Перем. 4 | Функция |
| x | ??? | ??? | ??? | F |
| 1 | 0 | 0 | 0 | 0 |
Строка №3: в ней один нуль — четвертый столбец. В исходном выражении, чтобы функция была ложна, необходимо, чтобы y = 0. Значит четвертый столбец соответствует переменной y.
| Перем. 1 | Перем. 2 | Перем. 3 | Перем. 4 | Функция |
| x | ??? | ??? | y | F |
| 1 | 1 | 1 | 0 | 0 |
Строка №2: в ней второй столбец равен единице, а третий — нулю. В исходном выражении ¬z ∧ w должно равняться 0, чтобы функция была ложной. Конъюнкция истинна только тогда, когда оба операнда истинны (равны 1); в нашем случае функция должна быть ложной, но пойдем от обратного. Если ¬z = 1, т.е. z = 0, а w = 1, то это неверно для нашего случая. Значит всё должно быть наоборот: z = 1, а w = 0. Таким образом столбец второй соответствует z, а столбец третий — w.
| x | z | w | y | F |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 | 0 |
| 1 | 1 | 1 | 0 | 0 |
Ответ: xzwy.













