Задача

Обозначим через ДЕЛ(n, m) утверждение «натуральное число n делится без остатка на натуральное число m».

Для какого наибольшего натурального числа А формула

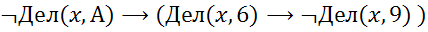
тождественно истинна (то есть принимает значение 1 при любом натуральном значении переменной х)?

Решение

Введем следующие обозначения:

Перепишим выражение в введенных обозначениях:

Выражение должно быть тождественно истино. Ключевым моментом в этой задаче является следующий факт:

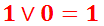
           (1)

    (2)

Для того, чтобы найти А необходимо инвертитовать (2). По закону Де-Моргана получим:

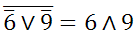
Поскольку в результате мы получили конъюнкцию (x одновременно делится на 6 и на 9), то необходимо найти наименьшее общее кратное:

разложим 6 на простые множители: 3 и 2;
разложим 9 на простые множители: 3 и 3.

Общий множитель 3, таким образом наименьшее общее кратное 3 x 3 x 2 = 18.

Ответ: 18.