Задача

На вход алгоритма подаётся натуральное число N. Алгоритм строит по нему новое число R следующим образом.

1. Строится двоичная запись числа N.
2. К этой записи дописываются справа ещё два разряда по следующему правилу:

а) складываются все цифры двоичной записи числа N, и остаток от деления суммы на 2 дописывается в конец числа (справа). Например, запись 11100 преобразуется в запись 111001;
б) над этой записью производятся те же действия – справа дописывается остаток от деления суммы её цифр на 2. Полученная таким образом запись (в ней на два разряда больше, чем в записи исходного числа N) является двоичной записью искомого числа R.

Укажите такое наименьшее число N, для которого результат работы данного алгоритма больше числа 77. В ответе это число запишите в десятичной системе счисления.

Решение

Проанализировав условие замечаем, что фактически к числу дважды дописывается бит чётности, причем уже после шага «а» у нас всегда получится чётное число единиц, поэтому шаг «б» всегда добавит ноль.

Если в конце двоичной записи числа стоит 0, значит, оно чётное, поэтому в результате работы алгоритма должно обязательно получиться чётное число. Поэтому мы будем рассматривать только четные числа.

Наименьшее четное число, которое превышает 77 - 78. Переведем его в двоичную систему счисления:

1001110 - результат работы алгоритма, число R. Исходное число N можно получить отбрасыванием двух последних разрядов в двоичной записи.

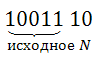
Переведем число N из двоичной системы счисления в десятичную:

Ответ: 19.