Задача
Для игры, описанной в задании 19, найдите минимальное значение S, при котором одновременно выполняются два условия:
– у Вани есть выигрышная стратегия, позволяющая ему выиграть первым или вторым ходом при любой игре Пети;
– у Вани нет стратегии, которая позволит ему гарантированно выиграть первым ходом.
Решение
Итак, нам необходимо найти такую проигрышную позицию, ходы из которой ведут в выигрышные позиции, среди которых есть такие, что Ваня не может выиграть за один ход, но может гарантированно выиграть за два (всего четыре хода):
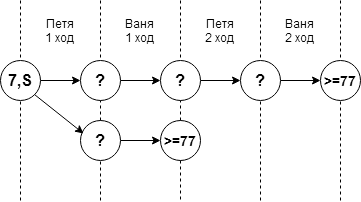
Это значит, что позиции, которые мы определили как выигрышные в задаче №20, яляются возможными исходами, после первого хода Пети, и выигрышными для второго хода Вани, а также, возможно, для первого хода Вани.
Для дальнейшего решения задачи построим таблицу выигрышных и проигрышных позиций. Выигрышные позиции будем обозначать положительными числами (2 – выигрыш в два хода), а проигрышные - отрицательными («–2» – проигрыш в два хода, второй игрок выиграет по крайней мере своим вторым ходом).
На вертикальной оси откладываем количество камней в первой куче, на горизонтальной – количество камней во второй куче. Расставим единицы в позициях, которые ведут к выигрышу Пети на первом ходу и «–1» в позициях, которые ведут к выигрышу Вани на своем первом ходу (после любого первого хода Пети):
Отметим числом 2 ячейки, откуда есть ход клетки с ходом «–1», в верхней строке таблицы выделим жёлтым позиции (7, 31) и (7, 34), найденные при решении предыдущего задания.
Нужно найти в первой строке позиции, из которых все ходы ведут в выигрышные позиции с кодами 1 (выигрыш за 1 ход) и 2 (выигрыш за 2 хода) одновлеменно.
Таких позиции (выделены зелёным цветом):
(7, 30) – возможные ходы в (7, 31), (8, 30) и (14, 30) с кодом 2 и (7, 60) с кодом 1
(7, 33) – возможные ходы в позиции (7, 34) и (8, 33) с кодом 2, а также (14, 33) и (7, 66) с кодом 1
Выбираем наименьше число - 30.
Ответ: 30.
По материалам К.Ю. Полякова.

















