Задача 15
На рисунке представлена схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И, К, Л, М. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой.
Сколько существует различных путей из города А в город М, проходящих через город Ж?
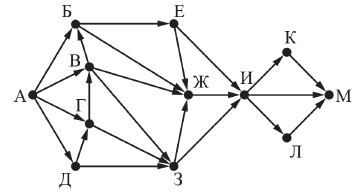
Удалим ребра, которые проходят «мимо» вершины Ж или до которых от пункта А можно дойти, минуя вершину Ж:
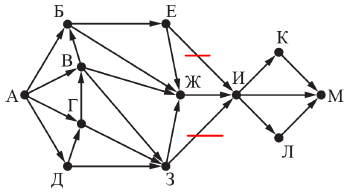
Теперь посчитаем результаты по оставшимся вершинам.
А = Д = 1
Г = А + Д = 1 + 1 = 2
В = А + Г = 1 + 2 = 3
З = В + Г + Д = 3 + 2 + 1 = 6
Б = А + В = 1 + 3 = 4
Е = Б = 4
Ж = Е + Б + В + З = 4 + 4 + 3 + 6 = 17
И = Ж = 17
Л = И = 17
К = И = 17
И = Ж = 17
М = К + Л + И = 51
Ответ: 51.













