Задача
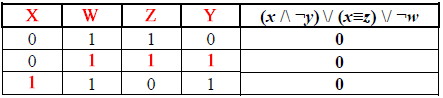
Миша заполнял таблицу истинности функции (x ∧ ¬y) ∨ (x≡z) ∨ ¬w, но успел заполнить лишь фрагмент из трёх различных её строк, даже не указав, какому столбцу таблицы соответствует каждая из переменных w, x, y, z.
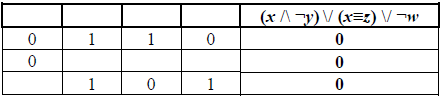Определите, какому столбцу таблицы соответствует каждая из переменных w, x, y, z.
Решение
Поскольку составное логическое выражение представлено из трех частей. соединенных дизъюнкцией — логическое сложение — то результат 0 может быть только тогда, когда все части выражения ложны:
| 1 часть | 2 часть | 3 часть | |||
| (x∧¬y) | ∨ | (x≡z) | ∨ | ¬w | = 0 |
1. (x ∧ ¬y) = 0
2. (x≡z) = 0
3. ¬w = 0
Построим таблицы истинности для всех трех частей выражения и выделим те строки, в которых функция действительно равны 0:
1. (x ∧ ¬y) = 0
| x | y | ¬y | F |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 0 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 0 |
2. (x≡z) = 0
| x | y | F |
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
3. ¬w = 0
| w | ¬w |
| 0 | 1 |
| 1 | 0 |
Учитывая соотношение значений переменных, объединим три таблицы, выбрав только подходящие строки.
| x | y | z | w | F |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 1 | 0 | 1 | 0 |
Так как w принимает только значение 1, то в исходной таблице ей соответствует столбец № 2.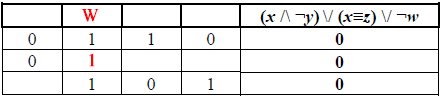 
В столбце №1 исходной таблицы имеем два нуля. В нашей таблице два нуля есть только в столбце с x. Таким образом, столбец №1 соответствует x.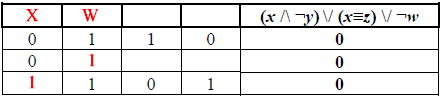 
Подставив значения, упомянутые выше, обратим внимание на строку №3 (т.к. если рассматривать строку №1, то в нашей таблице две строки с двумя звачениями 1). Получаем, что что z = 0, что соответствует столбцу №3.
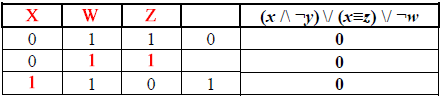Оставшийся столбец №4 - y.
Ответ: xwzy
