Проанализируем алгоритм.

В программе есть цикл, в котором переменная t принимает последовательно все целые значения в интервале от a до b:

for t:=a to b do begin
  ...
end;

До начала цикла в переменную M записывается значение a, а в переменную R – значение функции в точке a:

M:=a; R:=F(a); 

Внутри цикла есть условный оператор, в котором вычисляется значение функции F(t) и сравнивается со значением переменной R:

if (F(t)<R)then begin
  M:=t;
  R:=F(t);
end;

Если новое значение функции меньше, чем значение R, в R записывается значение функции в точке t, а в переменной M запоминается само значение t (аргумент функции, соответствующий значению в R).

В результате анализа можно сделать вывод, что цикл ищет минимум функции F(t) на интервале от a до b, и после выполнения цикла в переменной M оказывается значение аргумента t, при котором функция достигает минимума на заданном интервале (здесь это интервал [-20, 20]).

Функция, которая используется в программе, – это квадратичная парабола:

Её ветви направлены вверх (коэффициент при x⁴ положительный, равен 1), она имеет два минимума в точках x=-10 и x=10.

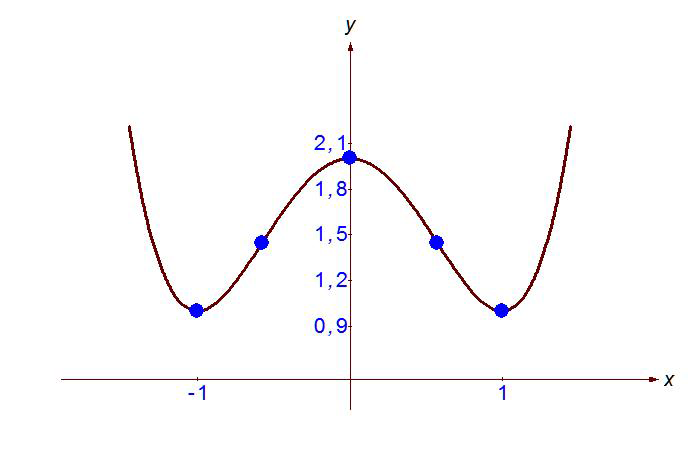
Внимание! График отображает суть квадратичной параболы и не является графиком рассматриваемой функции.

Обе точки минимума находятся на отрезке [-20;20], поэтому программа найдёт одну из этих точек; вопрос: какую именно?

Для квадратичной параболы обе точки минимума имеют одинаковую y-координату, а запоминание новой точки минимума происходит только тогда, когда только что вычисленное значение F(t) станет строго меньше, чем хранящееся в переменной R:

if (F(t) < R)then begin
  M:=t;
  R:=F(t);
end;

Поэтому в точке второго минимума никаких изменений не произойдет, и в переменной M останется значение «–10».

Обратим внимание, что на экран выводится не M, а M+27, поэтому результат будет равен:

Ответ: 17.