Задача 26
Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежат две кучи камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в одну из куч (по своему выбору) один камень или увеличить количество камней в куче в три раза. Например, пусть в одной куче 10 камней, а в другой 7 камней; такую позицию в игре будем обозначать (10, 7). Тогда за один ход можно получить любую из четырёх позиций: (11, 7), (30, 7), (10, 8), (10, 21). Для того чтобы делать ходы, у каждого игрока есть неограниченное количество камней.
Игра завершается в тот момент, когда суммарное количество камней в кучах становится не менее 68. Победителем считается игрок, сделавший последний ход, т.е. первым получивший такую позицию, при которой в кучах будет 68 или больше камней. В начальный момент в первой куче было 6 камней, а во второй куче - S камней; 1 ≤ S ≤ 61.
Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника. Описать стратегию игрока – значит описать, какой ход он должен сделать в любой ситуации, которая ему может встретиться при различной игре противника. В описание выигрышной стратегии не следует включать ходы играющего по этой стратегии игрока, не являющиеся для него безусловно выигрышными, т.е. не являющиеся выигрышными независимо от игры противника.
Выполните следующие задания.
Задание 1.
а) Укажите все такие значения числа S, выиграть за один ход.
б) Известно, что Ваня выиграл своим первым ходом после неудачного первого хода Пети. Укажите минимальное значение S, когда такая ситуация возможна.
Задание 2.
Укажите такое значение S, при котором у Пети есть выигрышная стратегия, причём одновременно выполняются два условия:
− Петя не может выиграть за один ход;
− Петя может выиграть своим вторым ходом независимо от того, как будет ходить Ваня.
Для указанного значения S опишите выигрышную стратегию Пети.
Задание 3.
Укажите значение S, при котором одновременно выполняются два условия:
− у Вани есть выигрышная стратегия, позволяющая ему выиграть первым или вторым ходом при любой игре Пети;
− у Вани нет стратегии, которая позволит ему гарантированно выиграть первым ходом.
Для указанного значения S опишите выигрышную стратегию Вани. Постройте дерево всех партий, возможных при этой выигрышной стратегии Вани (в виде рисунка или таблицы).
В узлах дерева указывайте позиции, на рёбрах рекомендуется указывать ходы. Дерево не должно содержать партии, невозможные при реализации выигрывающим игроком своей выигрышной стратегии. Например, полное дерево игры не является верным ответом на это задание.
Запишем условие более понятным языком.
Возможны два хода: +1, *3.
Изначально в одной куче было 6 камней, а в другой - S (1 ≤ S ≤ 61).
Победителем считается игрок, сделавший последний ход, т.е. первым получивший такую позицию, при которой в кучах будет 63 камня или больше.
Первым ходит Петя.
Задание 1а. Укажите все такие значения числа S, при которых Петя может выиграть за один ход.
Решение задания 1а. Если во второй куче было S камней, то после первого хода Пети количество камней в двух кучах может стать равным:
7+S (после добавления 1 камня в любую кучу);
18+S (после утроения первой кучи);
6+3S (после утроения второй кучи).
Выписываем условия выигрыша на первом ходу для всех трёх вариантов:
Отсюда следует, что при S ≥ 21 Петя выиграет первым же ходом, удвоив число камней во второй куче.
Ответ на задание 1а.
Петя может выиграть при 21 ≤ S ≤ 61
Задание 1б. Известно, что Ваня выиграл своим первым ходом после неудачного первого хода Пети. Укажите минимальное значение S, когда такая ситуация возможна.
Решение задания 1б. Очевидно, что любой ход Пети должен привести к ситуации 21 ≤ S ≤ 61, т.е. создана выигрышная ситуация (6, 21). Это возможно при Smax=20 (21-1) или при Smin=7 (21:3). Минимальное значение - 7.
Ответ на задание 1б.
S=7
Задание 2. Укажите такое значение S, при котором у Пети есть выигрышная стратегия, причём одновременно выполняются два условия:
− Петя не может выиграть за один ход;
− Петя может выиграть своим вторым ходом независимо от того, как будет ходить Ваня.
Для указанного значения S опишите выигрышную стратегию Пети.
Решение задания 2. Необходимо найти такое значение S (количество камней во второй куче), при котором Петя не сможет выиграть своим первым ходом, но и Ваня также не может выиграть своим первым ходом. Причем, любой ход Вани создает выигрышную ситуации для Пети, который выигрывает своим вторым ходом.
Одним из вариантов решения задания 1б была ситуация S (6, 20). Рассмотрим ее:
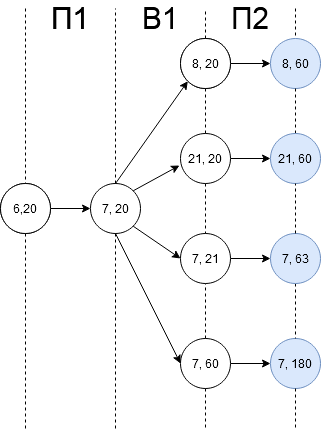
Примечание. На схеме буквами П1, В1 и т.д. указан первый ход Пети, первый ход Вани соответственно.
Таким образом, S=20.
Обратите внимание, что мы рассматривали только выигрышную позицию после первого хода Пети, рассматривать необходимо только ее (и только ее).
Ответ на задание 2.
S = 20. В этом случае Петя, очевидно, не может выиграть первым ходом. Однако он может получить позицию (7,20). После хода Вани может возникнуть одна из 4-х позиций: (8,20), (21,20), (7,21), (7,60). В каждой из этих позиций Петя может выиграть одним ходом, утроив количество камней во второй куче.
Примечание. В качестве ответа можно представить значение S и дерево всех возможных партий при выбранной стратегии Пети (см. рисунок выше).
Задание 3. Укажите значение S, при котором одновременно выполняются два условия:
− у Вани есть выигрышная стратегия, позволяющая ему выиграть первым или вторым ходом при любой игре Пети;
− у Вани нет стратегии, которая позволит ему гарантированно выиграть первым ходом.
Для указанного значения S опишите выигрышную стратегию Вани.
Постройте дерево всех партий, возможных при этой выигрышной стратегии Вани (в виде рисунка или таблицы).
В узлах дерева указывайте позиции, на рёбрах рекомендуется указывать ходы. Дерево не должно содержать партии, невозможные при реализации выигрывающим игроком своей выигрышной стратегии. Например, полное дерево игры не является верным ответом на это задание.
Решение задания 3. Необходимо найти S, причем обязательно учитывать условия:
- у Вани есть выигрышная стратегия (первым или вторым ходом) при любой игре Пети;
- первый ход не гарантированно выигрышный.
То есть, первая стратегия может быть выигрышная, может нет, но вторая – однозначно должна быть выигрышной.
S, при котором гарантированно можно выиграть вторым ходом – 20, позиция (6,20) (см. задание 2). Рассмотрим S = 19:
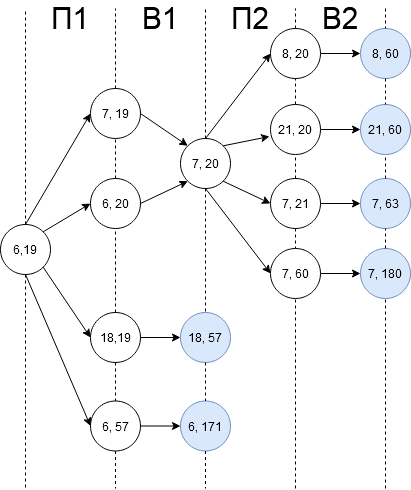
Ответ на задание 3.
S = 19. После первого хода Пети возможны позиции: (7,19), (18,19), (6,20), (6,57). В позициях (18,19) и (6,57) Ваня может выиграть первым ходом, утроив количество камней во второй куче. Из позиций (7,19) и (6,20) Ваня может получить позицию (7,20). Эта позиция разобрана в п.2. Игрок, который её получил (теперь это Ваня), выигрывает своим вторым ходом.
Далее должо быть представлено дерево всех возможных решений.
Также дерево решений может быть представленно в виде таблицы:
| Положение после очередных ходов | ||||
| Исходное положение | 1-й ход Пети (все возможные ходы) | 1-й ход Вани (указаны только ходы по стратегии) | 2-й ход Пети (все возможные ходы) | 2-й ход Вани (указаны только ходы по стратегии) |
| (6, 19) | (7, 19) | (7, 20) | (8, 20) | (8, 60) |
| (21, 20) | (21, 60) | |||
| (6, 20) | (7, 21) | (7, 63) | ||
| (7, 60) | (7, 180) | |||
| (18, 19) | (18, 57) | |||
| (6, 57) | (6, 171) | |||
ВНИМАНИЕ! Лишних фраз, рассуждений не касающихся сути вопроса, в ответе писать не нужно! В данном случае действует правило - "Что спросили, то и ответили".
Полный, верно оформленный ответ будет выглядеть следующим образом:
Задание 1а.
Петя может выиграть при 21 ≤ S ≤ 61
Задание 1б.
S=7
Задание 2.
{tab Вариант оформления 1}
S = 20. В этом случае Петя, очевидно, не может выиграть первым ходом. Однако, он может получить позицию (7,20). После хода Вани может возникнуть одна из 4-х позиций: (8,20), (21,20), (7,21), (7,60). В каждой из этих позиций Петя может выиграть одним ходом, утроив количество камней во второй куче.
{tab Вариант оформления 2}
S = 20.

{/tabs}
Примечание. Необходимо выбрать один из вариантов оформления ответа.
Задание 3.
{tab Вариант оформления 1}
S = 19. После первого хода Пети возможны позиции: (7,19), (18,19), (6,20), (6,57). В позициях (18,19) и (6,57) Ваня может выиграть первым ходом, утроив количество камней во второй куче. Из позиций (7,19) и (6,20) Ваня может получить позицию (7,20). Эта позиция разобрана в п.2. Игрок, который её получил (теперь это Ваня), выигрывает своим вторым ходом.

{tab Вариант оформления 2}
S = 19. После первого хода Пети возможны позиции: (7,19), (18,19), (6,20), (6,57). В позициях (18,19) и (6,57) Ваня может выиграть первым ходом, утроив количество камней во второй куче. Из позиций (7,19) и (6,20) Ваня может получить позицию (7,20). Эта позиция разобрана в п.2. Игрок, который её получил (теперь это Ваня), выигрывает своим вторым ходом.
| Положение после очередных ходов | ||||
| Исходное положение | 1-й ход Пети (все возможные ходы) | 1-й ход Вани (указаны только ходы по стратегии) | 2-й ход Пети (все возможные ходы) | 2-й ход Вани (указаны только ходы по стратегии) |
| (6, 19) | (7, 19) | (7, 20) | (8, 20) | (8, 60) |
| (21, 20) | (21, 60) | |||
| (6, 20) | (7, 21) | (7, 63) | ||
| (7, 60) | (7, 180) | |||
| (18, 19) | (18, 57) | |||
| (6, 57) | (6, 171) | |||
{/tabs}
Примечание. Необходимо выбрать один из вариантов оформления ответа.













